Авторы:   С. А. Алексеев, канд. техн. наук; А. В. Пасяда

Санкт-Петербургский государственный университет информационных технологий, механики и оптики, Санкт-Петербург

КРАТКИЙ ОБЗОР

Разработан метод распознавания формы поверхности по интенсивности и поляризации отраженного излучения. Распознавание проводится при известном характере освещения поверхности. На эталонном объекте определяются изменения интенсивности и поляризации излучения в зависимости от геометрии отражающей поверхности, а затем полученные данные позволяют восстанавливать форму произвольных поверхностей. Эти вычисления реализуются на ячеистой нейроподобной сети с помощью оптимизационного метода, основанного на принципе эволюции до глобального минимума функции энергии.

Введение
Зависимость отражения от ориентации поверхности
Алгоритм распознавания формы по затенению и поляризации
Результаты эксперимента
Заключение
Литература

ВВЕДЕНИЕ

Решение задачи распознавания формы поверхности по монокулярному изображению при известных параметрах освещения поверхности традиционно основано на использовании изменения интенсивности излучения.

Для повышения точности и улучшения распознавания границ между объектами предлагается также использовать параметры поляризации. Для этого схема установки осветитель — сцена с распознаваемыми объектами — наблюдатель дополняется осветителем поляризованного света и анализатором.

Процесс восстановления формы поверхности начинается с получения зависимости ориентации отражающей поверхности (или относительного расстояния до неё) из непрозрачного материала от яркости и поляризации на изображении эталонного объекта. Затем данная зависимость используется для восстановления форм произвольных объектов с соответствующими отражающими свойствами. В качестве метода восстановления формы с учётом параметров поляризации доработан оптимизационный подход поиска минимума функции энергии, представленный в статье [1].

Зависимость отражения от ориентации поверхности

Если в схеме установки технического зрения осветитель-сцена с распознаваемыми объектами-фотоприёмник задать угловое положение осветителя, сцены и фотоприёмника (видеокамеры), а также интенсивность освещающего поверхность пучка I₀, то можно получить характерную для данного материала зависимость отражательной способности R(Ψ, Ξ) от угла наклона Ψ и азимута наклона Ξ отражающей поверхности. Для восстановления формы важно получить зависимость интенсивности отраженного излучения (или яркости на изображении) от ориентации поверхности

Если поляризация излучения, освещающего объекты, также задана, то для задачи распознавания можно использовать параметры поляризации отраженного излучения, например, эллиптичность ε и азимут θ. Если получить зависимости I(Ψ, Ξ), ε(Ψ, Ξ) и θ(Ψ, Ξ) для исследуемого отражающего материала, то можно существенно приблизиться к решению задачи распознавания формы, т. е. к определению Ψ(I, ε, θ) и Ξ(I, ε, θ).

На исследуемых поверхностях имеет место зеркальное и диффузное отражение. При диффузном отражении поляризованный свет частично деполяризуется и в каждой точке растрового изображения определяется сумма эллипсов поляризации. Тем не менее азимут и эллиптичность такой фигуры также несут информацию об ориентации поверхности. Известно также, что при зеркальном отражении излучения компонент светового вектора E_p поглощается сильнее компонента E_s (рис. 1), что отражается на эллипсе поляризации отраженного луча. Такая же закономерность присутствует при диффузном отражении и может быть использована при распознавании.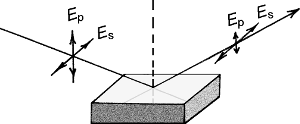

Рис. 1. Подавление р-компонента электрической напряженности излучения Е световой волны при зеркальном отражении.

Параметры поляризации вычисляются фотометрическим методом по ряду положений вращающегося анализатора. При этом используется бескомпенсаторная схема измерения поляризации. Схема установки на рис. 2 предполагает постоянной угол между осветителем, сценой с объектами и фотоприёмником и постоянное расстояние до сцены.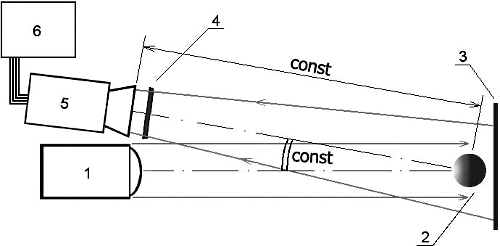

Рис. 2. Схема установки. 1 — осветитель с поляризованным излучением, 2 — объект, 3 — фоновый экран, 4 — вращающийся анализатор, 5 — видеокамера, б — ЭВМ, обрабатывающая изображения.

В этом случае метод распознавания состоит в следующем. Сначала с помощью эталонного объекта определяются зависимости интенсивности и поляризации от ориентации отражающей поверхности. По этим данным обучается нейроподобная сеть для распознавания произвольной формы. Подробнее эту процедуру можно представить как последовательность нескольких этапов.

1. Сцена освещается параллельным пучком линейно поляризованного света. Линейная поляризация используется из-за влияния деполяризации при отражении и особенностей бескомпенсаторной схемы измерения поляризации.
2. На сцену помещается эталонный объект из исследуемого материала. Объект выбран в форме шара, так как на шаре присутствуют все возможные ориентации поверхности и на нём просто определить ориентацию во всех точках. Распознавание шара на изображении рассматривается в [2].
3. На полученных изображениях определяется зависимость интенсивности I(Ψ, Ξ), азимута θ(Ψ, Ξ) и эллиптичности ε(Ψ, Ξ) от ориентации отражающей поверхности. Затем из Ψ вычисляется расстояние до поверхности z. Это относительное расстояние можно представить в единицах радиуса эталонного шара r, как

   z = r·(1 – cos(Ψ)).

   (2)

4. По данным зависимостям проводится обучение нейросети, восстанавливающей расстояние до поверхности z.
5. На сцену помещается произвольный объект с тем же материалом поверхности, и по изображению восстанавливается расстояние z.

Алгоритм распознавания формы по затенению и поляризации

Распознавание формы по затенению и отражённой поляризации, как одну из некорректно поставленных задач, можно свести к оптимизационной проблеме поиска минимума функции энергии, представляющей ошибку. Если рассматривать достаточно малую окрестность вокруг точки растра, то можно допустить наличие свойств случайных полей Маркова, т. е. полагать, что имеют место распределение Гиббса и связь значения I в точке растра (i, j) со значениями I в соседних точках (а также наличие связи между значениями ε и между значениями θ). Распределение значений в окрестности каждой точки изображения содержит важную информацию, поэтому локальная природа связей между нейронами реализуется в виде ячеистой нейроподобной сети (ЯНС), как это было представлено в работе [1]. Такая сеть представляет собой массив идентичных динамических ячеек, имеющих только локальные связи [3]. Любая ячейка соединена только со своими соседними ячейками, косвенное взаимодействие с остальными ячейками обусловлено распространяющимся эффектом динамики в сети. Ячейка C_ij, двумерного массива M×N имеет р-окрестность N^p_ij, размером (2р + 1)(2р + 1), где р — параметр размера окрестности. Схема ячейки дискретного по времени действия ЯНС показана на рис. 3.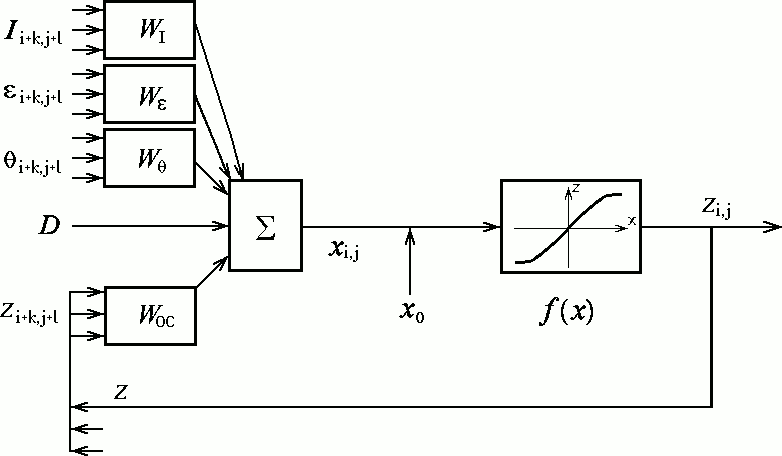

Рис. 3. Схема одной ячейки ячеистой нейросети.

На схеме ряд значений на входе I_i+k,j+l, ε_i+k,j+l и θ_i+k,j+l (где k = i – р, i – р + 1, ...,i + р; а l = j – р, j – р + 1, ..., j + р) умножаются на весовые коэффициенты матриц W_I, W_ε и W_θ. В связи с особенностями угловой величины азимута θ_i+k,j+l, среднее значение θ' по окрестности N^p_ij предлагается определять векторной суммой. Для этого величина θ_i+k,j+l представлена в виде направления единичного вектора, умноженного на весовой коэффициент w_θ,i+k,j+l матрицы W_θ. Результат θ'_i,j определяется направлением вектора суммы таких векторов по окрестности N^p_ij. На рис. 3 x_ij — внутреннее состояние ячейки C_ij, x₀ — первоначальное внутреннее состояние при итерации t = 0, D — постоянное смещение на входе, W_ОС — матрица весовых коэффициентов обратной связи. Значение расстояния до поверхности на выходе определяется функцией активации z_ij(t) = f(x_ij(t)), где f(x) может быть любой подходящей нелинейной функцией. В работе выбрана сигмоидная функция с крутизной γ:

Такая система ЯНС является видом рекуррентной модели Хопфилда, но требует синхронного режима, только локальных связей с соседними нейроподобными элементами и использования переменных, непрерывно меняющихся в диапазоне [0; 1]. В такой динамической системе нейросети градиент хорошо определён и можно применить классические оптимизационные алгоритмы. При использовании подходящей функции энергии устойчивость ЯНС может быть доказана так же, как в непрерывной сети Хопфилда.

Как показано в работе [4], единственный путь вычислить z — это минимизировать функцию энергии Е, которая в данном случае определяется как

E = {ka·[(zij – zi + 1, j)2 + (zij – zi, j + 1)2 + (zij – zi – 1, j)2 + (zij – zi, j – 1)2] + kb·|(zij – z'ij)/z'ij|},

(4)

Минимум энергии можно вычислить, используя или алгоритмы стохастической релаксации, например, метод "имитации отжига", или детерминистические алгоритмы, например, алгоритм итеративных условных моделей [5].

Для определения расстояния z рассматривается изображение эталонного шара, на основе которого предстоит получить зависимости I(z) ε(z) и θ(z). В результате распознавания границы эталонного объекта на растровом изображении определяется область пикселов с известными значениями наклона поверхности Ψ и параметрами I, ε и θ. По формуле (2) для известного значения Ψ определяется z. Строится однослойная ЯНС с числом нейроподобных элементов, равным числу точек изображения эталонного объекта.

Из квадратной окрестности N^p_ij на вход каждого нейрона подаются значения I, ε и θ. В данном эксперименте у всех нейронов C_ij были выбраны одинаковые матрицы весовых коэффициентов 7×7 (матрицы для входных значений интенсивности W_I, для эллиптичности W_ε, для азимута поляризации W_θ и для обратной связи W_ОС).

В методе "имитации отжига" на первом шаге весовые коэффициенты принимаются равными нулю, вычисляется энергия Е₀, температура T₀, отвечающая за вероятность изменения весов, берётся высокой. Методом "имитации отжига" вычисляются весовые коэффициенты [6] по описанному далее алгоритму.

1. D и x₀ изменяются с вероятностью P_D = P_x0 = 0,4 на шаг ±Δw_D. В зависимости от температуры T веса́ интенсивности w_I, эллиптичности w_ε, азимута w_θ и обратной связи w_ОС случайно изменяются на шаг ±Δw с вероятностью

2. На первой итерации t = 1 на вход нейрона С_i,j подаются значения выборки I_{i + k,j + l}, ε_{i + k,j + l}, θ_{i + k,j + l} и D и вычисляется выходное значение z_ij. На следующих итерациях t нейрон учитывает также значения от обратных связей. В работе [1] показано, что можно добиться хорошего схождения алгоритма при 3–4 итерациях t.

3. Используя уравнение (4), вычисляется функция энергии E. Если энергия уменьшилась, то шаг 1 принят и весовые коэффициенты сохраняются. Если энергия увеличилась, то изменения в шаге 1 могут быть приняты с вероятностью

4. Если энергия уменьшилась, то температура уменьшается в a_T  раз

Эти шаги обучения нейросети повторяются до достижения порога E'.

(Em – 1 – Em)/En < E'

(8)

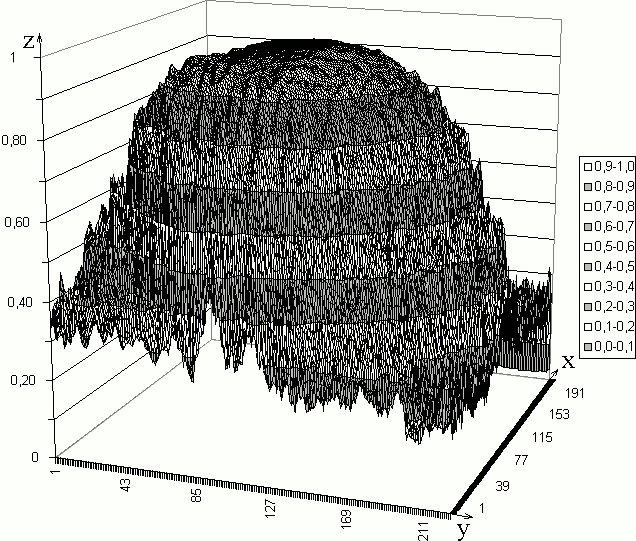
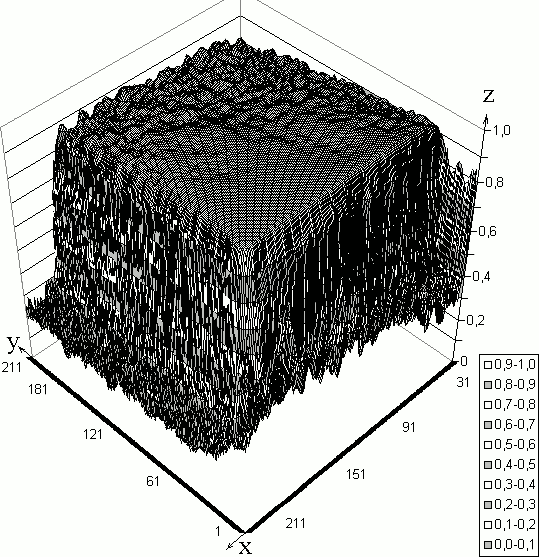
Затем можно уменьшить шаг изменения весов Δw и снова проводить вычисления до получения значений E_n, удовлетворяющих неравенству (8).

Результаты эксперимента

На основе фотометрического метода определения поляризации в каждой точке растра на созданном программном обеспечении [7] было обработано изображение шара и кубика-угла, окрашенных серой нитроэмалью. Измерение поляризации проходило по четырём положениям анализатора — 0°, 45°, 90° и 135°. При этом интенсивность нормирована к 1 (0 ≤ I ≤ 1), шаги изменения всех весовых коэффициентов Δw = ±0,002, начальная температура T₀ = 9, T' = 1, а_T = 0,9999, порог для изменения энергии Е' = 10^–5, коэффициенты в функции энергии k_b = 1 и k_a = 1, крутизна функции активации γ = 0,13.

Для шара (рис. 4а) и куба (рис. 5a), окрашенных серой нитроэмалью, были рассчитаны значения относительного расстояния до поверхности (рис. 4б и 56). В результате распознавания средняя ошибка определения этого расстояния в случае шара составила 28,3% при размере изображения эталонного объекта 250×250 точек и 11,8% при размере 50×50 точек. Это позволяет предположить, что для увеличения скорости обучения и повышения точности следует проводить обучение нейросети на малом объёме данных с пониженной детализацией изображения (это грубое и быстрое приближение к глобальному минимуму энергии), а затем провести дообучение на полной выборке.

a	б

Рис. 4. а — изображение калибровочного шара, б — распознанная поверхность, расстояние (1 – z) в единицах радиуса поверхности.

a	б

Рис. 5. а — изображение куба, б — распознанная поверхность куба.

Заключение

В статье представлен метод распознавания трёхмерной формы поверхности, который решает задачу получения зависимости параметров отражённой световой волны от ориентации поверхности эталонного объекта и задачу восстановления формы поверхностей по полученной зависимости. Для решения задачи восстановления были рассмотрены особенности реализации оптимизационного процесса, основанного на поиске глобального состояния минимума функции энергии. Практическая реализация этого процесса проводится на ячеистой нейроподобной сети, которая определяет относительное расстояние поверхности, однозначно связанное с наклоном уравнением (2), с помощью программного обеспечения [7]. Результаты эксперимента позволили определить расстояние до поверхности со средней погрешностью 28,5 и 11,8% при 62500 и 2500 точках обучающей выборки соответственно. Следует отметить относительную устойчивость метода распознавания к шумам на изображении. В отличие от [1] благодаря особенностям схемы установки в рассмотренном методе не возникает проблемы расчёта угла падения света.

Следует отметить, что полученные результаты согласуются с литературными данными. Тем не менее обработка поляризации расширяет, возможности систем технического зрения, что может быть в дальнейшем использовано для различения материалов и обнаружения сложных визуальных явлений на объектах.

Литература

1. Milanova M, Almeida P. Е. M, Okamoro J., Simões M G. Applications of Cellular Neural Networks for Shape from Shading Problem. Lecture Notes in Artiftcial Intelligence // Machine Learning and Data Mining in Pattern Recognition. 1999. Р. 51 – 63. [Примечание — русскоязычный перевод этой статьи размещён на странице в Интернете http://teh-zren.ru/st-jans.htm]

2. Алексеев С.А., Пасяда А.В. Распознавание глубины по затенению и поляризации // Научно-технич. вестник СПбГУИТМО. 2006. В. 26. С. 81 – 86.

3. Chua L.О., Roska T. The CNN Paradigm // IEEE Transactions on Circuits and Systems (Part1). 1993. V, 40. № 3. Р. 147 – 156

4. Koch С., Marroquin J., Yuille А. Analog Neural Networks in Early Vision // Proc. Natl. Acad. Sci. USA. 1986. V. 83. Р. 4263–4267.

5. Besag J. On the Statistical Analysis of Dirty Pictures // J.R. Statist. Soc. В. 1986. V. 48. № 3. Р. 259 – 302.

6. Заенцев О.В. Нейронные сети: основные модели. Учебное пособие Воронежск. Гос. ун-та. 2000. 30 с.

7. Пасяда А.В. Программное обеспечение "Поляризация на калибровочном шаре" http://ralertmod.narod.ru/p.htm [Примечание: в настоящий момент эти функции выполняет обновлённая версия этой программы под названием "Просмотрщик поляризационных изображений, полученных фотометрическим методом" (PIRPhM viewer); он размещён на странице в Интернете http://teh-zren.ru/programmy.htm#pirphm]